-
Noteiktā integrāļa tuvināta aprēķināšana ar Gausa kvadrātu formulām
| Nr. | Название главы | Стр. |
| Ievads | 4 | |
| Noteiktā integrāļa jēdziens | 5 | |
| Gausa kvadrātu formulas | 6 | |
| Optimālas formulas konstruēšana | 6 | |
| Kvadrātu formula jebkurai lineārai funkcijai | 7 | |
| Ležandra polinomi | 7 | |
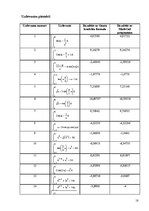
| Gausa kvadrātu formulas mezgli un svaru koeficienti | 8 | |
| Kvadrātu formulas izpēte | 9 | |
| Gausa kvadrāta formula ar diviem mezgliem | 10 | |
| Gausa kvadrāta formula ar trijiem mezgliem | 11 | |
| Piemērs | 12 | |
| Gausa kvadrātu formula integrāliem ar robežu [a,b] | 12 | |
| Rēķināšanas piemērs | 13 | |
| Datorprogramma | 15 | |
| Svaru koeficienti un mezgli Gausa kvadrātu formulai | 15 | |
| Lietotāja interfeis | 16 | |
| Programmas realizācija | 17 | |
| Uzdevumu piemēri | 20 | |
| Secinājumi | 22 | |
| Izmantota literatūra | 23 |
Ievads
Skaitliskās analīzes pamatā ir matemātiskā modeļa izstrāde, tā algoritmizēšana, realizācija uz datora un rezultātu analīze. Kā galveno skaitļošanas matemātikas sastāvdaļu var izdalīt skaitliskās metodes, bez kurām nav iedomājama matemātiskā modelēšana.
Reķinot fiziskus un tehniskus uzdevumus vajag meklēt noteiktus integrālus no funkcijam, kurus nav tik viegli izteikt ar elementāram funkcijam. Un tas pievēda pie nepieciešamības atrast tuvinātas formulas lai atrisināt noteiktus integrālus.
Savā referātā es apskatīju tādu tēmu, ka Gausa kvadrātu formulas, tos izmantošanu noteikta integrāļa tuvināta aprēķināšanā. Sākumā es nedaudz paskaidroju kas tas ir integrāls, pēc tam jau aprakstīju Gausa kvadrātu formulas.
Bet praktiskājā daļā man bija nepieciešams izveidot datorprogrammu, ar kuras palīdzību paradīt ka integrāļi tiek rēķināti, izmantojot Gausa formulas. Programmu es uzrakstīju C# valodā un lai to palaist ir nepieciešams Framework 1.1.
…
Par noteiktā integrāļa jēdzienu un par Gausa kvadrātu formulam