| Nr. | Название главы | Стр. |
| 1. | Kaudze (Heap sort) | 4 |
| 1.1. | Pārskats | 4 |
| 1.2. | Kas ir kaudze | 4 |
| 1.3. | Kaudzes algoritms (mazākā elementa izmešana) | 5 |
| 1.4. | Kārtošana ar kaudzi (Heap Sort) | 7 |
| 1.5. | Kaudzes kārtošanas algoritms | 7 |
| 1.6. | Kaudzes kārtošanas algoritma realizācija C++ | 9 |
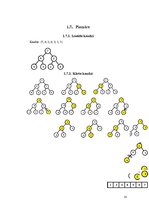
| 1.7. | Piemērs | 10 |
| 1.7.1. | Izveido kaudzi | 10 |
| 1.7.2. | Kārto kaudzi | 10 |
| Secinājumi | 11 | |
| Izmantotais izziņas avotu saraksts | 12 |
1.4. Kārtošana ar kaudzi (Heap Sort)
Ja rindu ar prioritāti realizējam ar kaudzes palīdzību, tad nav nepieciešama papildus atmiņa, t.i. kaudzi var realizēt tajā pašā tabulā, kurā atrodas kārtojamie elementi. Indekss i tabulā nosaka robežu starp sakārtoto un nesakārtoto tabulas daļu. Kaudze ir realizēta nesakārtotajā daļā: intervālā A[i..n-1]. Kaudzes sakne (mazākais elements) atrodas labajā pusē pozīcijā A[n-1]. Līdz ar to kaudze dilst no kreisās puses, bet sakārtotā daļa, aizņemot kaudzes atbrīvoto vietu, pieaug no labās puses. Indekss i pavirzās pa labi un nosaka jauno robežu.
Algoritma ideja: samainām kaudzes sakni ar pašu kreisāko elementu nesakārtotajā daļā un veicam kaudzes "atjaunošanas darbus" ar procedūras Heapify palīdzību. Darbojoties ar kaudzi algoritmā Heapify ir jāatceras, ka atšķirībā no kaudzes standartrealizācijas tabulā (no kreisās uz labo), šoreiz kaudze ir apgriezta otrādi (no labās uz kreiso).
…
Kaudze ir binārs koks ar elementiem, kuriem ir piekārtota prioritāte, un mezgli ir sakārtoti tā, ka katra mezgla (elementa) prioritāte ir mazāka vai vienāda salīdzinot ar bērnu prioritātēm. Līdz ar to kaudzes (koka) augšā ir elements ar vismazāko prioritāti un uz jebkura ceļa kokā mezgli ir sakārtoti pieaugošā kārtībā.